• 1 Basics
  • 1.1 GCC中-l, -L和-I参数的解释
    • 1.1.1 编译过程
    • 1.1.2 预处理中包含头文件
    • 1.1.3 链接库
  • 1.2 Compiler options
    • 1.2.1 -Wl,-rpath,.
    • 1.2.2 LD_LIBRARY_PATH and LDFLAGS
• 2 Advanced
  • 2.1 Floating operation
    • 2.1.1 Precision loss
  • 2.2 Misc
    • 2.2.1 Compile MPICH using GCC version 10

1 Basics

1.1 GCC中-l, -L和-I参数的解释

1.1.1 编译过程

如图¹所示，分为四个步骤：预处理 -> 编译 -> 汇编 -> 链接

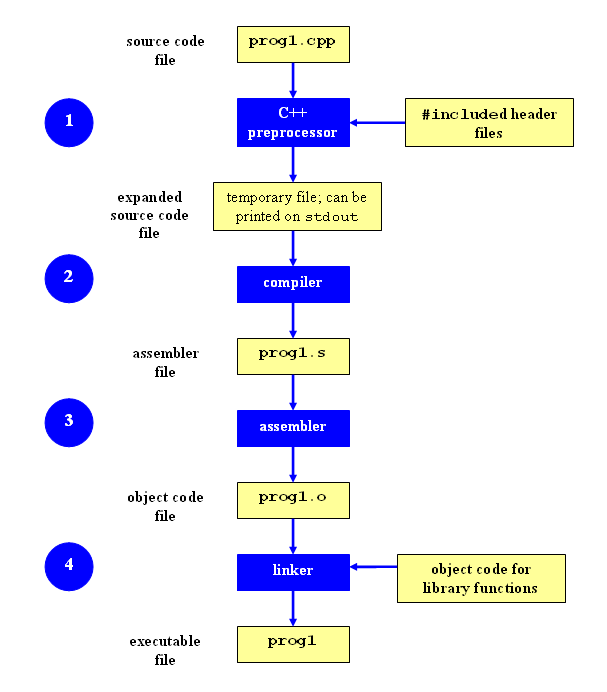
1.1.2 预处理中包含头文件

-I参数是用来指定头文件目录，/usr/include 目录一般是不用指定的，gcc知道去那里找，但是如果头文件不在/usr/include里我们就要用-I参数指定了，比如头文件放在/myinclude目录里，那编译命令行就要加上-I/myinclude参数了，如果不加你会得到一个xxxx.h: No such file or directory的错误。-I参数可以用相对路径，比如头文件在当前目录，可以用-I.来指定。

1.1.3 链接库

1.1.3.1 基本含义

-l参数就是用来指定程序要链接的库，-l参数紧接着就是库名。那么库名跟真正的库文件名有什么关系呢？就拿数学库来说，他的库名是m，他的库文件名是libm.so，很容易看出，把库文件名的头lib和尾.so去掉就是库名了。

1.1.3.2 使用方法

好了现在我们知道怎么得到库名，当我们自已要用到一个第三方提供的库名字libtest.so，那么我们只要把libtest.so拷贝到/usr/lib里，编译时加上-ltest参数，我们就能用上libtest.so库了（当然要用libtest.so库里的函数，我们还需要与libtest.so配套的头文件）。

1.1.3.3 指定库文件位置

放在/lib和/usr/lib和/usr/local/lib里的库直接用-l参数就能链接了，但如果库文件没放在这三个目录里，而是放在其他目录里，这时我们只用-l参数的话，链接还是会出错，出错信息大概是：/usr/bin/ld: cannot find -lxxx，也就是链接程序ld在那三个目录里找不到libxxx.so，这时另外一个参数-L就派上用场了，比如常用的X11的库，它在/usr/X11R6/lib目录下，我们编译时就要用-L/usr/X11R6/lib -lX11参数，-L参数跟着的是库文件所在的目录名。再比如我们把libtest.so放在/aaa/bbb/ccc目录下，那链接参数就是-L/aaa/bbb/ccc -ltest

1.2 Compiler options

1.2.1 -Wl,-rpath,.

The -Wl,xxx option for gcc passes a comma-separated list of tokens as a space-separated list of arguments to the linker. So

gcc -Wl,aaa,bbb,ccc

which eventually becomes a linker call

ld aaa bbb ccc

In your case, you want to say ld -rpath ., so you pass this to gcc as -Wl,-rpath,. or -Wl,-rpath -Wl,..

1.2.2 LD_LIBRARY_PATH and LDFLAGS

LD_LIBRARY_PATH is used at runtime not compile time to find the correct libraries. You need to set LDFLAGS or set a configure option to find the library.

2 Advanced

2.1 Floating operation

2.1.1 Precision loss

With the debug mode -O0 -g, gfortran gives inaccurate result of the following code snippet while Intel compiler is OK.

usp_ngb(1) = matmul(extrapneighcell_mat(1, 1:9), usp_ghs(1:9, 1))

And the data are as follows. With the help of IEEE-754 Floating-Point Conversion: From 64-bit Hexadecimal Representation To Decimal Floating-Point. The hex number of usp_ghs are 0x[4005d800daac1039, 3ffe80007746d2d2, 4000e6006365931d, 401fdf4953631862, 400566edb9b4edd3, 3ffc162669b0c434, 4018836ece868caa, 401eaa5c4c981115, 400976c7ef0d2624]. The corresponding double precision floating values are [2.7304703792342733, 1.9062504443401633, 2.1123054280636910, 7.9680531529648720, 2.6752581127491140, 1.7554077271017947, 6.1283523816702345, 7.6663677184881370, 3.1829985309493782] The hex number of extrapneighcell_mat are 0x[4018000000008a60, c02000000000769b, 400800000000c5ad, 0, 0, 0, 0, 0, 0]. The corresponding double precision floating values are [6.0000000000314630, -8.0000000000539360, 3.0000000000224730, 0, 0, 0, 0, 0, 0]

Use the raw hex number to do multiplication in this website: Floating Point Multiplication/Division.

4018000000008a60 * 4005d800daac1039 = 
Round to Zero
A*B  + 1.0000011000100000000010100100000000010110101010011111 *24 = 16.382822275491545
Round to Nearest Even
A*B  + 1.0000011000100000000010100100000000010110101010100000 *24 = 16.38282227549155
Round to Plus Infinity
A*B  + 1.0000011000100000000010100100000000010110101010100000 *24 = 16.38282227549155
Round to Minus Infinity
A*B  + 1.0000011000100000000010100100000000010110101010011111 *24 = 16.382822275491545

c02000000000769b * 3ffe80007746d2d2 = 
Round to Zero
A*B  - 1.1110100000000000000001110111010001111011010011101001 *23 = -15.25000355482412
Round to Nearest Even
A*B  - 1.1110100000000000000001110111010001111011010011101001 *23 = -15.25000355482412
Round to Plus Infinity
A*B  - 1.1110100000000000000001110111010001111011010011101001 *23 = -15.25000355482412
Round to Minus Infinity
A*B  - 1.1110100000000000000001110111010001111011010011101010 *23 = -15.250003554824122

400800000000c5ad * 4000e6006365931d = 
Round to Zero
A*B  + 1.1001010110010000000010010101000110010010110101110010 *22 = 6.3369162842385425
Round to Nearest Even
A*B  + 1.1001010110010000000010010101000110010010110101110010 *22 = 6.3369162842385425
Round to Plus Infinity
A*B  + 1.1001010110010000000010010101000110010010110101110010 *22 = 6.3369162842385425
Round to Minus Infinity
A*B  + 1.1001010110010000000010010101000110010010110101110010 *22 = 6.3369162842385425

With the python mpmath package, it shows that with rounding to the neatest even mode, the final accurate result should be

from mpmath import mp, mpf, matrix
mp.dps = 32
mpf('16.38282227549155') + mpf('-15.25000355482412') + mpf('6.3369162842385425')
Out[67]: mpf('7.4697350049059724999999999999999923')

gfortran gives usp_ngb(1) = 7.469735004905969 while the Intel compiler gives 7.4697350049059708. Thus the Intel compiler gives more accurate result. Note that both gfortran enables -fno-unsafe-math-optimizations -frounding-math and Intel compiler enables -fp-model fast. Changing to -fp-model precise does not change the value.

With -fno-rounding-math, the rounding mode is known to be round to even. With -frounding-math, it is round-to-zero for all floating point to integer conversions, and round-to-nearest for all other arithmetic truncations.

In gfortran, setting -frounding-math -fsignaling-nans lead to full IEEE 754 compliance. “Support infinities, NaNs, gradual underflow, signed zeros, exception flags and traps, setting rounding modes. Compare with C99’s #pragma STDC FENV ACCESS ON. Warning! GCC currently assumes that the same rounding mode is in effect everywhere”.

Probably this error is due to the rounding in the intermediate calculation. Intel compiler uses more digits to ensure the double precision while gfortran probably requires additional compilation flag to do that. For details, maybe check Different floating point result with optimization enabled - compiler bug?.

Reference

• Semantics of Floating Point Math in GCC

2.2 Misc

2.2.1 Compile MPICH using GCC version 10

export FFLAGS="-w -fallow-argument-mismatch -O2"

Reference: Bug 91731 - Configure error on building MPICH

---

1. The C++ compilation process↩︎